古希腊人将数学视为一切知识的基础，同时也是哲学的重要思想源泉之一。其中，毕达哥拉斯不仅发现了黄金分割比0.618和1.618，还发现了有形状的数字。

形数即有形状的数。公元前6世纪，希腊的毕达哥拉斯学派研究数的概念时，常常把数描绘成沙滩上的小石子，用它们进行各式各样的排列和分类，叫做“形数”。

用3颗石子可以摆成一个正三角形，同样用6颗石子或者10颗石子可以摆成更大的三角形。因此，毕达格拉斯学派把1,3,6,10等叫作“三角数”或“三角形数”。

用4颗，9颗或16颗石子都能摆成正方形，因此把1,4,9,16等叫作“正方形数”。

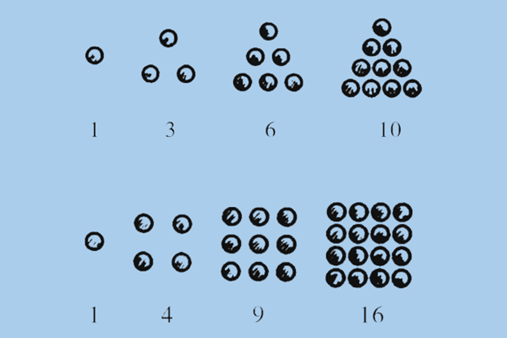
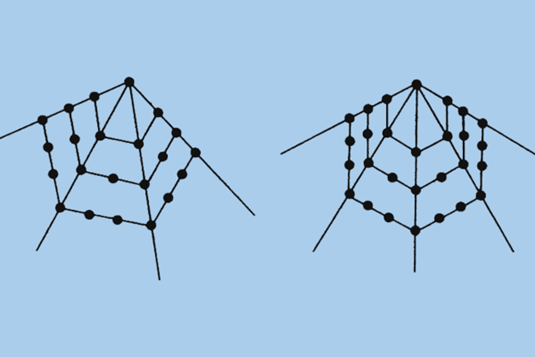
他们还摆出了五边形数、六边形数和其他多边形数。

毕达哥拉斯学派还进一步发掘了各种数间的内在联系。比如，任意两个相邻的三角形数相加，必然是一个数的平方，也就是必须是一个正方形数。

反过来，每个正方形数都可以分成相邻的两个三角形数。

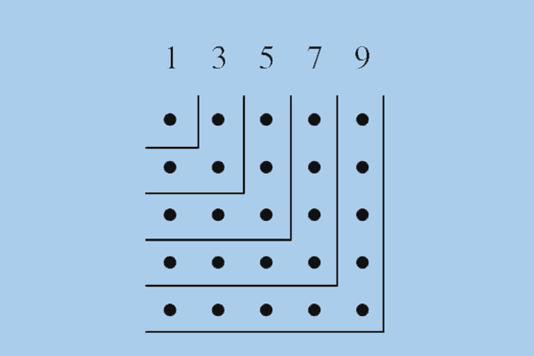
利用正方形数可以造出一个奇数表：1,3,5,7,9……

他们在正方形格子里放上石子，放法是最上面一行和最左边一列都按1，2,3……来放石子。其他空格中的石子数，等于对应的最上面一行和最左边一列两格石子数之积。他们把这种拐角形叫“磐折形”。每一个磐折形中所有数之和是一个立方数。

他们还发现，在弹奏乐器时，弦所发出的声音的频率和琴弦的长度有关。同时，他们把天文现象归于数字，认为行星的运动会发出声音，而且行星运动所产生的天籁之音一定是和谐的。

不过，毕达哥拉斯为世人所知，主要是因为一个著名的发现：三角形的两个直角边长度的平方和，等于斜边长度的平方．这个在我国被称为勾股定理的数学规律，在西方一直被称为毕达哥拉斯定理。

据说是，一天毕达哥拉斯在浴室洗澡的时候，从浴室的地砖上发现了这个定理。他迫不及待地把这个定理告诉了他的学生希帕索斯，他指出，无论直角三角形的形状大小如何变化，每个直角三角形的两条直角边长度的平方和都等于斜边长度的平方。

关于形数，你有没有更了解一些呢？

本文由中国人民大学附属中学第二分校一级教师秦薇进行科学性把关。

新华网科普事业部

科普中国-科学原理一点通

联合出品

更多精彩内容，请下载科普中国客户端。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。